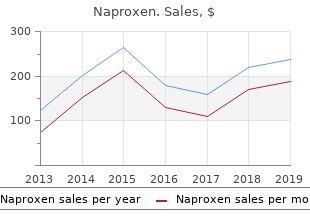
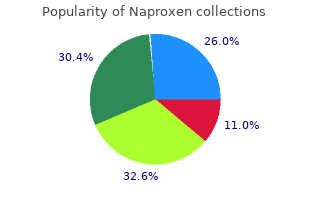
North Carolina Agricultural and Technical State University. V. Fraser, MD: "Buy Naproxen. Discount online Naproxen no RX.".

The sampling distribution of means is the frequency distribution of all possi- ble sample means that occur when an infinite number of samples of the same size N are randomly selected from one raw score population cheap naproxen 500 mg mastercard arthritis in both ring fingers. This is similar to a distribution of raw scores order naproxen with a visa arthritis pain groin area, except that here each score on the X axis is a sample mean safe naproxen 500 mg arthritis in the knee cure. To the right of are the sample means the statistician obtained that are greater than 500, and to the left of are the sample means that were less than 500. This is because most scores in the population are close to 500, so most of the time the statistician will get a sample containing scores that are close to 500, so the sample mean will be close to 500. Less frequently, the statistician will obtain a strange sample containing mainly scores that are farther below or above 500, producing means that are farther below or above 500. Once in a great while, some very unusual samples will be drawn, resulting in sam- ple means that deviate greatly from 500. The story about the bored statistician is useful because it helps you to understand what a sampling distribution is. The central limit theorem is a statistical principle that defines the mean, the standard deviation, and the shape of a sampling distribution. From the central limit theorem, we know that the sampling distribution of means always (1) forms an approximately normal distribution, (2) has a equal to the of the underlying raw score population from which the sampling distribution was created, and (3), as you’ll see shortly, has a standard deviation that is mathematically related to the standard deviation of the raw score population. The importance of the central limit theorem is that with it we can describe the sam- pling distribution from any variable without actually having to infinitely sample the population of raw scores. Then we’ll know the important characteristics of the sampling distribution of means. Remember that we took a small detour, but the original problem was to evaluate our Prunepit mean of 520. To do so, we simply determine where a mean of 520 falls on the X axis of the sampling distribution in Figure 6. But if 520 lies toward the tail of the distribution, far from 500, then it is a more infrequent and unusual sample mean (the statistician seldom found such a mean). The sampling distribution is a normal distribution, and you already know how to determine the location of any “score” on a normal distribution: We use—you guessed it—z-scores. That is, we determine how far the sample mean is from the mean of the sampling distribution when measured using the standard deviation of the distribution. This will tell us the sample mean’s relative standing among all possible means that occur in this situation. To calculate the z-score for a sample mean, we need one more piece of information: the standard deviation of the sampling distribution. The Standard Error of the Mean The standard deviation of the sampling distribution of means is called the standard error of the mean. That is, in some sampling distributions, the sample means may be very different from one another and, “on average,” deviate greatly from the average sample mean. For the moment, we’ll discuss the true standard error of the mean, as if we had actually computed it using the entire sampling distribution. The σ indicates that we are describing a population, but the subscript X indicates that we are describing a population of sample means—what we call the sampling dis- tribution of means. The central limit theorem tells us that σX can be found using the following formula: The formula for the true standard error of the mean is σX σX 5 1N Using z-Scores to Describe Sample Means 127 Notice that the formula involves σX, the true standard deviation of the underlying raw score population, and N, our sample size. This is because with more variable raw scores the statistician often gets a very different set of scores from one sample to the next, so the sample means will be very different (and σX will be larger). But, if the raw scores are not so variable, then different samples will tend to contain the same scores, and so the means will be similar (and σX will be smaller). With a very small N (say 2), it is easy for each sample to be different from the next, so the sample means will differ (and σX will be larger). How- ever, with a large N, each sample will be more like the population, so all sample means will be closer to the population mean (and σX will be smaller). This is because the bored statisti- cian will often encounter a variety of high and low scores in each sample, but they will usually balance out to produce means at or close to 500.

According to our experiences naproxen 500mg for sale arthritis diet stories, recreational therapy can help icine purchase naproxen 250mg online erosive arthritis definition, Kuala Lumpur buy generic naproxen 500mg on line arthritis in back and legs, Malaysia, 3University Malaya, Rehabilitation disabled dementia patients improve or maintain their functional Medicine Department, Kuala Lumpur, Malaysia and psychological status. The authors believe that the programs can apply not Introduction/Background: Diabetic Charcot foot can cause gross only to hospital-based day care center, but also in non-hospital- structural deformities of the foot and ankle, and subsequent skin based day care centers. Chung have equal study is to explore complications of diabetic charcot foot in particu- contribution to this poster. Moridnia 1Shahid Beheshti University of Medical Sciences, Clinical Re- mortality rate during the follow-up period was 15. The mean survival time based on Kaplan- Maier Survival Analysis search Development Center of Shahid Modarres Hospital and is 44. The remaining 83 alive sample population Physical Medicine and Rehabilitation Research Center, Tehran, (84. Conclusion: Recurrent new philosophy which tries to lead clinical services to effective and ulcer in Charcot foot patients has high predilection towards limb advantageous ways with the least side effects and errors. Members of faculty, participants who referrals from all states in Malaysia for intensive spinal rehabilita- had attended workshops and physicians who spent more time on tion program or other specialised rehabilitation programs that are research and article review had more knowledge (p=0. Hence, epidemiology data on spinal cord 3 most common sources used for research were PubMed, Google injured patients that was analysed in this study should represent scholar and Cochrane, respectively. Material and Methods: cal practice, the most common source used was reference books Data on all new patients admitted to Spinal Rehabilitation Ward in (86. Analysis was done on the incidence, with getting access to associated databases and lack of suffcient age, gender and level of injury. Results: From Aug 2014 until Nov activity in judging and analyzing related articles. Age group of the studied population are as shown in with its concepts and applications. It may also of benefts for effcient resource allocation for the rehabilitation management of spinal cord injured 1Thomas Jefferson University, Rehabilitation Medicine, Philadel- patients in Malaysia. Material and Methods: The authors reviewed a sample of 220 discharges from J Rehabil Med Suppl 55 Poster Abstracts 237 Thomas Jefferson University Hospital rehabilitation unit readmit- to prevent absenteeism due to sickness. Readmissions were categorized as: (1) from the reha- questionnaire focusing on the organizational setting and its impact bilitation hospital to the acute hospital or (2) from the community on employee wellbeing – reported as mental energy, work-related to the acute care hospital. The questionnaire measures good into categories to provide meaningful information to implement and poor work environment factors to help managers improve or- policies to minimize readmissions. The questionnaire was validated qualitatively plete management, (2) recurrences, and (3) development of new and quantitatively. Cases with new conditions: thors followed a company undergoing organizational change and 36 (73%. Cases with ers uncertain about employee mental status can measure employee new conditions: (54%). Cases with incomplete care or recurrences: wellbeing easily and cost effectively to prevent illness. Conclusion: (1) Most of the cases were readmitted to created a method, statistically evaluated, to proactively identify acute hospitals before completion of their rehabilitation hospital good and poor work Environments to promote healthy co-workers. Japan, 2Fujita Health University, School of Medicine, Toyoake, Hashemi2 Japan, 3Fujita Health University Hospital, Department of Reha- 1 bilitation, Toyoake, Japan, 4Fujita Health University Banbuntane Physical Medicine and Rehabilitation Research Center of Shahid Beheshti University of Medical Sciences and Clinical Research De- Hotokukai Hospital, Department of Rehabilitation, Nagoya, Japan velopment Center of Shahid Modarres Hospital, Physical Medicine 2 Introduction/Background: Previous studies have shown that toe and Rehabilitation, Tehran, Iran, Physical Medicine and Reha- clearance during the swing phase affects the risk of tripping; this bilitation Research Center of Shahid Beheshti University of Medi- is considered a predominant cause of falls. In healthy subjects, toe cal Sciences, Physical Medicine and Rehabilitation, Tehran, Iran, clearance is obtained mainly by lower limb movements. However, 3Arak University of Medical Sciences-Vali-Asr Hospital, Physical in stroke patients, the compensatory movements are more important Medicine and Rehabilitation, Tehran, Iran in obtaining toe clearance. The purpose of this preliminary study is to clarify the system of obtaining toe clearance in stroke patients in Introduction/Background: Trend to non surgical treatments in mus- comparison to healthy subjects. Material and Methods: Thirteen pa- plications and studies in Iran have been started about 15 years ago. A motion analysis system, the Kinema- in musculoskeletal disorders in Iran from 2000 and 2015. Material Tracer® (Kissei Comtec, Nagano), was used for the kinematic anal- and Methods: A review of literatures in Google scholar, PubMed, ysis of the gait. Then was conducted to fnd the difference between the patients with hemi- studies which were related to musculoskeletal disorder were selected.

There was no 302 signifcant risk factor in our patient related to her stress fracture discount naproxen 250mg overnight delivery arthritis medication gold. While aging and post-menopausal period are well- Training Hospital buy naproxen 250 mg visa arthritis bruising, Physical Medicine and Rehabilitation purchase naproxen toronto arthritis neck lump, Istanbul, known reasons of osteoporosis; chronic illnesses and drug-induced Turkey conditions are not too easily remembered. Here we report a patient with osteoporotic ver- kyphosis of the thoracic or thoracolumbar spine. Material and Methods: A 47-year-old male patient by wedge shaped vertebral bodies, irregularities of the vertebral admitted to our outpatient clinic with 2-month history of back pain. He have been using le- is more common and involves a thoracic kyphotic pattern, often vetirasetam 500 mg twice daily and valproic acid 500 mg twice with nonstructural compensatory hyperlordosis of the lumbar daily for seven years due to epileptic seizures. There was no abnormality Material and Methods: Case: We report the case of a 30-yr-old in laboratory investigations regarding secondary reasons of osteo- man with a history of chronic cervical, mid-dorsal and low back porosis. Results: We diagnosed the patient as drug-induced osteo- pain, aggravated by standing, with no history of trauma. The possibility of other causes such as vitamin D age-sex matched healthy controls aged between 55–85 were includ- defciency, release of excess growth hormone or infections was ed in the study. Vitamin D def- Zotović”, Department of Child Rehabilitation, Banjaluka, Bosnia ciency was found in 89. Pathohistological fnding confrmed the 1Dıskapı Yıldırım Beyazıt Education and Research Hospital, Physi- diagnosis of eosinoflic granuloma. This signs were present at habilitation Center, Department of Physical Therapy and Rehabili- boy’s frst visit to physical medicine specialist after surgery: the tation, Ankara, Turkey boy couldn’t walk on his right heel, he couldn’t perform full active dorsal fexion in right talo-crural joint. Antefexion in the lumbar Introduction/Background: There is no clear correlation between segment of the spine was reduced to a greater extent. Similarly, vitamin D levels of the patients, even in early stages, Aydemir2 were lower than in controls and vitamin D levels reduced further 1Dıskapı Yıldırım Beyazıt Education and Reserach Hospital, Physi- with increasing duration of the disease. Nakanami Introduction/Background: It was suggested that posture train- 1Kanazawa Medical University, Rehabilitation Medicine, Uchi- ing support with spinal orthosis including weighted kyphorthosis nada, Japan, 2Tonami General Hospital, Rehabilitation Medicine, can improve balance in patients with osteoporosis. The aim of Tonami, Japan this study was to determine the effects of weighted kyphorthosis on improving dynamic balance tests in women with osteoporosis. A new method patients were assigned into two groups: 1) control group who re- for estimating in vivo bone mineral density and characterizing the ceived 4-week home-based daily exercise program and 2) inter- shape of cancellous bone has been proposed using the result of ul- vention group (weighted kyphorthosis) who performed exercises trasonic inspection for the diagnosis of osteoporosis. Patients Methods: The method is based on two-dimensional bone area frac- were assessed using computerized balance tests by Balance Master tions (percent bone area between bone and bone marrow) calculat- (NeuroCom) (Limits of Stability, Step Quick Turn, Sit to Stand and ed from the difference in the speed of ultrasonic wave propagation Walk across tests) before and 4 weeks after start of treatment. Improvement in right turn time in step quick characterization is based on the image simulation procedure em- turn, end point excursion and mean of excursion parameters of ploying eight random variable from a computer and the statistical Limits of Stability was more signifcant in orthosis group in com- result of fractal analysis for numerous cancellous bone patterns. Conclusion: This ultrasonic testing confrmed the presence of an effective intervention in postmenopausal women in order to re- local osteoporosis on the affected side of the hemiplegics as well duce the risk of falling. Material and Methods: One hundred and forty four women Introduction/Background: Obesity is a chronic disease that results were divided into four groups according to the time past meno- from metabolic disorders of energy homeostasis. All groups were subdivided development of diabetes or high blood pressure, but also diseases of into osteoporosis group (t-score <–2. We have examined 59 patients, of which there osteoporosis group compared to non-osteoporosis group but there were 43 women and 16 men. C-telopeptide was increased in os- exam the patients were divided into 3 groups (≥29. Conclusion: No specifc biochemi- tained results for patients in each group are differed in subsequent cal markers regarding the duration of menopause were found. Hip (femoral head), Knee (femoral condyle), Tibia can be considered as one of the factors infuencing on behavior of and Metatarsal bone are the affected sites. Khachnaoui1 consultation is especially paralysis of the extensors of the fngers 1Sahloul Hospital, Rehabilitation, Sousse, Tunisia and thumb ulnar extensor carpi. Material and Methods: A 35 year old patient, who is a farmer, without any particular medical history Introduction/Background: Achondroplasia is the most common consulted for a weakness in his left hand to progressive appearance inherited bone dysplasia. Electromyographic exami- We report the case of a young woman with achondroplasia which nation objectifed conduction block on the forearm posterior interos- presented paraplegia by spinal stenosis. Histological examination confrmed the diagnosis of lipoma from low back pain radiating to both legs and not systematized. Results: The evolution after 6 months of rehabilitation She had diffculty in micturition with leaks evolving for several was marked by improvement of symptoms and pain.

Obviously buy 250mg naproxen with visa arthritis in back and spine, if the observed and expected values are similar order naproxen us arthritis alternative treatments, then the chi-square value will be close to zero and therefore will not be significant purchase 250mg naproxen visa rheumatoid arthritis and lungs. The larger the observed and expected values are from one another, the larger the chi-square value becomes and the more likely the P value will be significant. This sample was not selected randomly and therefore only percentages will apply and the terms incidence and prevalence cannot be used. However, chi-square tests are valid to assess whether there are any between-group differences in the proportion of babies with certain characteristics. Question: Are males who are admitted for surgery more likely than females to have been born prematurely? Null hypothesis: That the proportion of males in the premature group is equal to the proportion of females in the premature group. Variables: Outcome variable = prematurity (categorical, two levels) Explanatory variable = gender (categorical, two levels) The command sequence to obtain a crosstabulation and chi-square test is shown in Box 8. Crosstabs Gender Recoded * Prematurity Crosstabulation Prematurity Premature Term Total Gender recoded Male Count 33 49 82 % within gender recoded 40. In this example, the sample size is too small for the chi-square distribution to approxi- mate the exact distribution of the Pearson statistic and so the Pearson chi-square value should not be reported. The Fisher’s exact test would be reported in this study because the sample size is only 141 children. This result can be reported as ‘Fisher’s exact test indicated that there was a significant difference in prematurity between males and females (40. The larger the difference between the rates in two groups, the smaller the sample size required to show a statistically significant difference. It is useful to include the 95% confidence intervals when results are shown as figures because the degree of overlap between them provides an approximate significance of the differences between groups. The interpretation of the degree of overlap is discussed in Chapter 3 (also see Table 3. Many statistics programs do not provide confidence intervals around frequency statis- tics. However, 95% confidence intervals can be easily computed using an Excel spread- √ sheet. The standard error around a proportion is calculated as [p(1–p)∕n] where p is Rates and proportions 259 the proportion expressed as a decimal number and n is the number of cases in the group from which the proportion is calculated. An Excel spreadsheet in which the percentage is entered as its decimal equivalent in the first column and the number in the group is entered in the second column can be used to calculate confidence intervals as shown in Table 8. The formula for the standard error is entered into the formula bar of Excel as sqrt (p × (1 − p)/n) and the formula for the width of the confidence interval is entered as 1. This width, which is the dimension of the 95% confidence interval that is entered into SigmaPlot to draw bar charts with error bars, can then be both subtracted and added to the proportion to calculate the 95% confidence interval values shown in the last two columns of Table 8. The calculations are undertaken in proportions (decimal numbers) but are easily con- verted back to percentages by multiplying by 100, that is, by moving the decimal point two places to the right. Using the converted values, the result could be reported as ‘the percentage of male babies born prematurely was 40. This was significantly different than the percentage of female babies born prematurely which was 20. Because the value of ‘n’ is integral in the denominator of the calculation of confidence intervals, the larger the sample size, the smaller the confidence will be, indicating greater precision in the result. In general, a large sample size is required to reduce 95% confidence intervals below a width of 5%. The lack of overlap between the confidence intervals is an approximate indication of a statistically significant difference between the two groups (see Table 3. Research question Question: Are the babies born in regional centres (away from the hospital or overseas) more likely to be premature than babies born in local areas? Null hypothesis: That the proportion of premature babies in the group born locally is not different to the proportion of premature babies in the groups born regionally or overseas. Variables: Place of birth (categorical, three levels and) prematurity (categorical, two levels) In this research question, there is no clear outcome or explanatory variable because both variables in the analysis are characteristics of the babies. This type of question is asked when it is important to know about the inter-relationships between variables in the data set. If prematurity has an important association with place of birth, this may need to be taken into account in multivariate analyses. The row percentages in the Crosstabulation table show that there is a difference in the frequency of prematurity between babies born at different locations.

Cheap naproxen american express. Joint pain relief in just one week | Joron k dard ka ilaaj.